yyyyyyyyyyyyy
Semaine du 6/11/23
Une lentille mince c’est une lentille où genre l’épaisseur de la lentille e est très petite devant les rayons de courbure de ses faces et aussi devant la distance entre les 2 centres de courbure
Vacances de Toussaint (23/10/23 et 30/10/23)
Théorème de décomposition de Dunford : https://5demi.fr/cours/maths/#reduction
Semaine du 16/10/23
Semaine du 9/10/23
semaine de dodo
Semaine du 2/10/23
semaine oisive
Semaine du 25/9/23
Informatique
Algo de Moore (pas essentiel) :
Au début, I c’est les états non finals, et II c’est les états finals (et pas « finaux »)
Puis on voit après lecture d’une lettre il va vers quelle partition et on le note
on fait ça pour toutes les lettres
et on fait le constat : lesquelles ont la même signature ??? (ie les même ->partitions + même partition avant)

voir https://www.desmontils.net/emiage/Module209EMiage/c5/Ch5_9.htm
Semaine du 18/9/23
Semaine du 11/9/23
Maths
\(\mathcal{R}\) est une relation d’équivalence sur un ensemble \(E\) ssi elle est :
\(\bullet\) réflexive : \( \forall x \in E \), \( x\mathcal{R}x\)
\(\bullet\) symétrique : \( \forall (x, y) \in E^2 \), \( x\mathcal{R}y \Leftrightarrow y\mathcal{R}x \)
\(\bullet\) transitive : \( \forall (x, y, z) \in E^3 \), \( x\mathcal{R}y \text{ et } y\mathcal{R}z \Rightarrow x\mathcal{R}z \)
Anglais
Roe v. Wade (1973) : States can no longer decide that abortion is unconstitutional.
And it was overtuned last year (June 2022)
Semaine du 4/9/23
Maths
\((G, \ast)\) est un groupe ssi
\(\bullet\) \(\ast\) est une LCI
\(\bullet\) \(e \in G\)
\(\bullet\) \(\forall x \in G, x^{-1} \in G\)
\(\bullet\) associativité
\((A, +, \times)\) est un anneau ssi
\(\bullet\) \((A, +)\) est un groupe abélien
\(\bullet\) \(\times\) est une LCI
\(\bullet\) \(1 \in A\)
\(\bullet\) associativité du \(\times\)
\(\bullet\) distributivité
\((K, +, \times)\) est un corps ssi
\(\bullet\) \((K, +)\) est un groupe abélien
\(\bullet\) \((K\backslash\{0\}, \times)\) est un groupe abélien
\(\bullet\) distributivité
Remarque
parfois on impose pas le commutatif pour \( (K\backslash\{0\}, \times) \), ça dépend des définitions
Physique
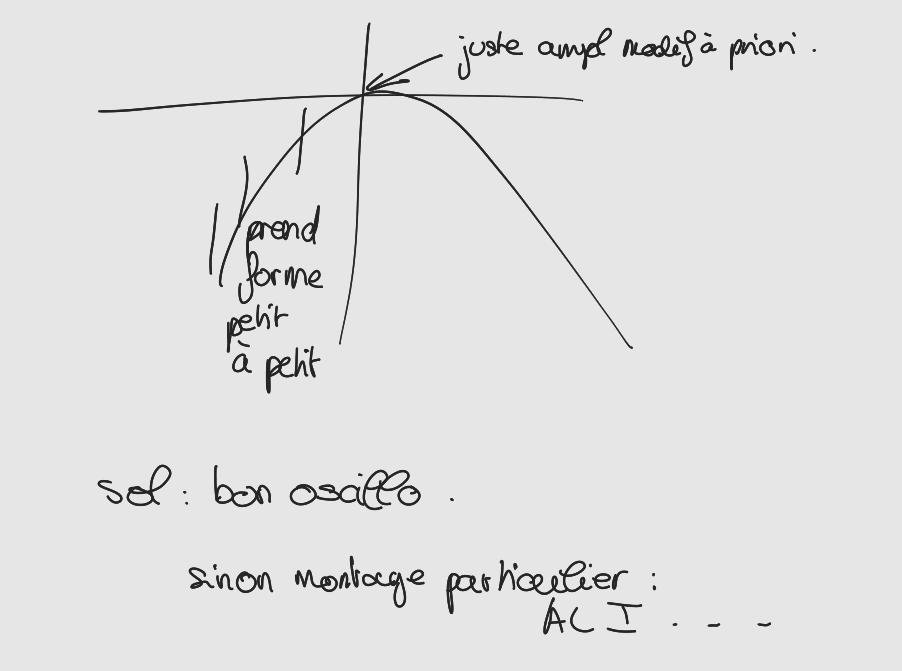
Pour régime sinusoïdal :
\(e(t) = E\cos(wt + \varphi_0)\)
\(s(t) = S\cos(wt + \varphi_0′)\)
On a
$$S = |H(x)|E $$
et
$$ \varphi_0′ = \varphi_0 + \varphi(x)$$
Sinon voici 2 intégrations usuelles :